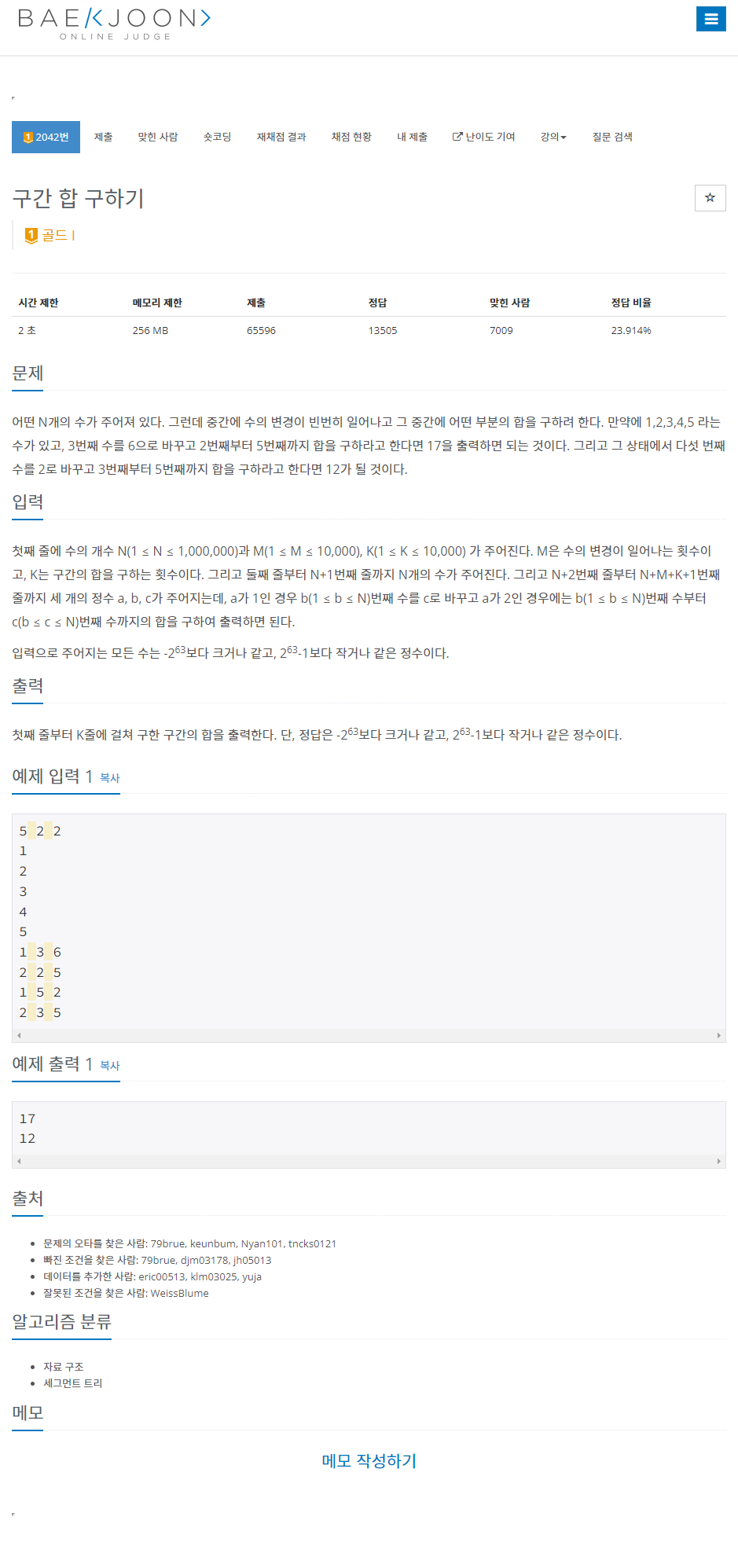
문제
2042 구간 합 구하기
풀이
- Long형 data를 최대 1,000,000개 합쳐야 하는 문제이다.
- 단순한 sum으로는 timeout이 발생한다.(아래 오답 부분 참고)
- 구간의 합을 구하기 위해 segment tree를 이용한다.
- Segment Tree는 부모 노드의 값이 자식 노드 값을 합이 되는 완전 이진 트리이다.
- 즉, root 노드는 전체 값의 합이 되고, leaf 노드는 각 값이 된다.
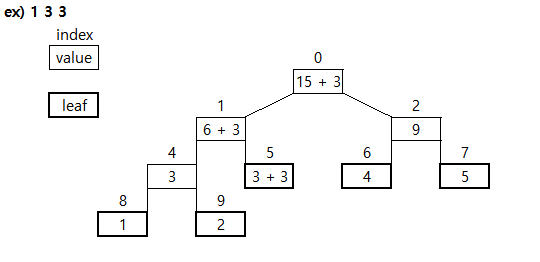
Step by Step (문제의 예제 입력 1)
값을 배열로 입력 받는다.
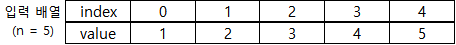
세그먼트 트리 배열을 만든다.
- 트리 배열의 크기: tn = 2 * 2⌈ log2n ⌉ - 1 = 17
- 간단하게 계산을 하기 위해서는: tn = 4 * n - 1 = 19으로 계산하여도 된다. 배열이 더 넉넉하게 생성되어 약간의 메모리 낭비가 생긴하는 단점이 있다.
- 배열의 빈칸은 비워둔다.
- n이 2의 거듭 제곱수(n = 2x)이면 트리는 포화 이진트리(Perfect Binary Tree)가 되면서 배열이 꽉 차게 되지만, 그 외의 경우 배열의 빈 칸이 생긴다.
- 트리 형태로 나타내면 아래 그림과 같이 된다.
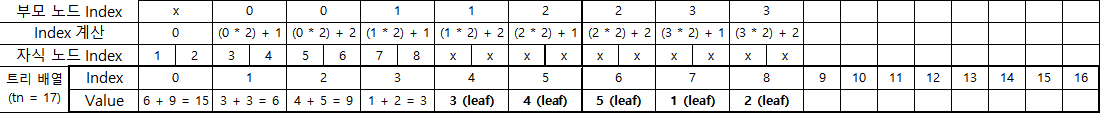
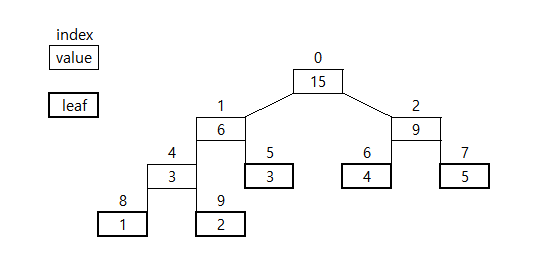
- kotlin code
private fun createTree(arr:LongArray) = LongArray(arr.getTreeSize()).let {
initTree(0, arr.lastIndex, arr, 0, it)
it
}
private fun LongArray.getTreeSize() = Math.pow(2.0, kotlin.math.ceil(kotlin.math.log2(this.size.toDouble()))).toInt() * 2 - 1
private fun initTree(arrStartIndex: Int, arrEndIndex:Int, arr:LongArray, nodeIndex:Int, tree:LongArray): Long {
if(arrStartIndex == arrEndIndex) {
tree[nodeIndex] = arr[arrStartIndex]
return tree[nodeIndex]
}
val arrMidIndex = getArrMidIndex(arrStartIndex, arrEndIndex)
val leftChildNode = initTree(arrStartIndex, arrMidIndex, arr, getNodeLeftChildIndex(nodeIndex), tree)
val rightChildNode = initTree(arrMidIndex + 1, arrEndIndex, arr, getNodeRightChildIndex(nodeIndex), tree)
tree[nodeIndex] = leftChildNode + rightChildNode
return tree[nodeIndex]
}
private fun getArrMidIndex(arrStartIndex: Int, arrEndIndex: Int) = (arrStartIndex + arrEndIndex) / 2
private fun getNodeLeftChildIndex(nodeIndex: Int) = nodeIndex * 2 + 1
private fun getNodeRightChildIndex(nodeIndex: Int) = getNodeLeftChildIndex(nodeIndex) + 1
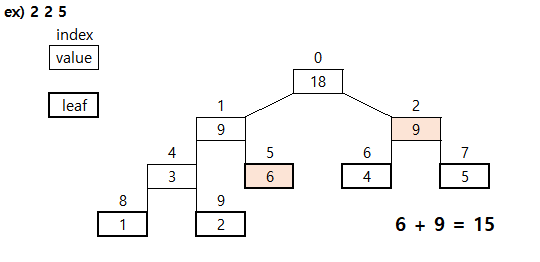
update
- root 노드 부터 해당 leaf 노드까지 기존 새로운 값과 기존 값의 차이를 더한다.
- kotlin code
private tailrec fun update(arrStartIndex: Int, arrEndIndex: Int, nodeIndex: Int, tree: LongArray, arrChangeIndex: Int, diffValue: Long) {
tree[nodeIndex] += diffValue
if(arrStartIndex == arrEndIndex) return
val arrMidIndex = getArrMidIndex(arrStartIndex, arrEndIndex)
if(arrChangeIndex <= arrMidIndex)
update(arrStartIndex, arrMidIndex, getNodeLeftChildIndex(nodeIndex), tree, arrChangeIndex, diffValue)
else
update(arrMidIndex + 1, arrEndIndex, getNodeRightChildIndex(nodeIndex), tree, arrChangeIndex, diffValue)
}
private fun getArrMidIndex(arrStartIndex: Int, arrEndIndex: Int) = (arrStartIndex + arrEndIndex) / 2
private fun getNodeLeftChildIndex(nodeIndex: Int) = nodeIndex * 2 + 1
private fun getNodeRightChildIndex(nodeIndex: Int) = getNodeLeftChildIndex(nodeIndex) + 1
sum
- 합을 구하기 위한 인덱스 범위안에 노드가 있으면 이용하여 합을 구한다.
- kotlin code
private fun sum(arrStartIndex:Int, arrEndIndex:Int, sumStartIndex:Int, sumEndIndex:Int, node:Int, tree:LongArray): Long {
if(sumStartIndex <= arrStartIndex && arrEndIndex <= sumEndIndex) return tree[node]
val arrMidIndex = getArrMidIndex(arrStartIndex, arrEndIndex)
val leftSum = if(sumStartIndex <= arrMidIndex) sum(arrStartIndex, arrMidIndex, sumStartIndex, sumEndIndex, getNodeLeftChildIndex(node), tree) else 0L
val rightSum = if(sumEndIndex > arrMidIndex) sum(arrMidIndex + 1, arrEndIndex, sumStartIndex, sumEndIndex, getNodeRightChildIndex(node), tree) else 0L
return leftSum + rightSum
}
답
kotlin code: 오답 - (당연하게도)timeout
fun main() {
val (n, m, k) = readln().split(' ').map { it.toInt() }
val array = LongArray(n) { readln().toLong() }
repeat(m + k) {
val strArray= readln().split(' ')
when(strArray[0].toInt()) {
1 -> array[strArray[1].toInt()-1] = strArray[2].toLong()
2 -> println((strArray[1].toInt()-1 until strArray[2].toInt()).sumOf { array[it] })
}
}
}
kotlin code: 정답 - Segment Tree 사용
fun main() {
val (n, m, k) = readln().split(' ').map { it.toInt() }
val arr = LongArray(n) { readln().toLong() }
val tree = createTree(arr)
repeat(m + k) {
val strArray= readln().split(' ')
when(strArray[0].toInt()) {
1 -> {
val index = strArray[1].toInt()-1
update(0, n-1, 0, tree, index, strArray[2].toLong() - arr[index])
arr[index] = strArray[2].toLong()
}
2 -> println(sum(0, n-1, strArray[1].toInt()-1, strArray[2].toInt()-1, 0, tree))
}
}
}
private fun createTree(arr:LongArray) = LongArray(arr.getTreeSize()).let {
initTree(0, arr.lastIndex, arr, 0, it)
it
}
private fun LongArray.getTreeSize() = Math.pow(2.0, kotlin.math.ceil(kotlin.math.log2(this.size.toDouble()))).toInt() * 2 - 1
private fun initTree(arrStartIndex: Int, arrEndIndex:Int, arr:LongArray, nodeIndex:Int, tree:LongArray): Long {
if(arrStartIndex == arrEndIndex) {
tree[nodeIndex] = arr[arrStartIndex]
return tree[nodeIndex]
}
val arrMidIndex = getArrMidIndex(arrStartIndex, arrEndIndex)
val leftChildNode = initTree(arrStartIndex, arrMidIndex, arr, getNodeLeftChildIndex(nodeIndex), tree)
val rightChildNode = initTree(arrMidIndex + 1, arrEndIndex, arr, getNodeRightChildIndex(nodeIndex), tree)
tree[nodeIndex] = leftChildNode + rightChildNode
return tree[nodeIndex]
}
private fun sum(arrStartIndex:Int, arrEndIndex:Int, sumStartIndex:Int, sumEndIndex:Int, nodeIndex:Int, tree:LongArray): Long {
if(sumStartIndex <= arrStartIndex && arrEndIndex <= sumEndIndex) return tree[nodeIndex]
val arrMidIndex = getArrMidIndex(arrStartIndex, arrEndIndex)
val leftSum = if(sumStartIndex <= arrMidIndex) sum(arrStartIndex, arrMidIndex, sumStartIndex, sumEndIndex, getNodeLeftChildIndex(nodeIndex), tree) else 0L
val rightSum = if(sumEndIndex > arrMidIndex) sum(arrMidIndex + 1, arrEndIndex, sumStartIndex, sumEndIndex, getNodeRightChildIndex(nodeIndex), tree) else 0L
return leftSum + rightSum
}
private tailrec fun update(arrStartIndex: Int, arrEndIndex: Int, nodeIndex: Int, tree: LongArray, arrChangeIndex: Int, diffValue: Long) {
tree[nodeIndex] += diffValue
if(arrStartIndex == arrEndIndex) return
val arrMidIndex = getArrMidIndex(arrStartIndex, arrEndIndex)
if(arrChangeIndex <= arrMidIndex)
update(arrStartIndex, arrMidIndex, getNodeLeftChildIndex(nodeIndex), tree, arrChangeIndex, diffValue)
else
update(arrMidIndex + 1, arrEndIndex, getNodeRightChildIndex(nodeIndex), tree, arrChangeIndex, diffValue)
}
private fun getArrMidIndex(arrStartIndex: Int, arrEndIndex: Int) = (arrStartIndex + arrEndIndex) / 2
private fun getNodeLeftChildIndex(nodeIndex: Int) = nodeIndex * 2 + 1
private fun getNodeRightChildIndex(nodeIndex: Int) = getNodeLeftChildIndex(nodeIndex) + 1